Advertisements
Advertisements
Question
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones.
Solution
Let the number of cones be n.
Let the radius of the sphere be rs =6 cm
Radius of a cone be rc =2 cm
And the height of the cone be h =3 cm
A volume of sphere = n(Volume of a metallic cone)
`=> 4/3 pir_s^3 = n(1/3 pir_c^2 h)`
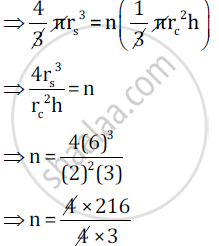
n = 72
Hence, the number of cones is 72.
APPEARS IN
RELATED QUESTIONS
On a map drawn to a scale of 1: 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
1) the actual length of the diagonal distance AC of the plot in km.
2) the actual area of the plot in sq. km.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
Find the surface area of a sphere of radius 5.6 cm .
Find the surface area of a sphere of diameter 14 cm .
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm.
(Use 𝜋 = 3.14)
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved
surface area of the shape if the length of the shape be 7 cm.
The surface area of a sphere is 2464 cm2, find its volume.
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm?
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r cm.
Determine the ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube.
Find the total surface area of a hemisphere of radius 10 cm.
Find the radius of a sphere whose surface area is 154 cm2.
The volume of a sphere is 905 1/7 cm3, find its diameter.
The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.
