Advertisements
Advertisements
Question
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r cm.
Solution
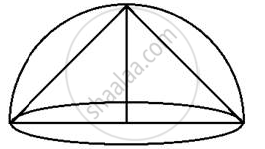
For the volume of cone to be largest, h = r cm
Volume of the cone
= `1/3pir^2h`
= `1/3pi xx r^2 xx r`
= `1/3pir^3`
APPEARS IN
RELATED QUESTIONS
A right circular cylinder just encloses a sphere of radius r (see figure). Find
- surface area of the sphere,
- curved surface area of the cylinder,
- ratio of the areas obtained in (i) and (ii).

A model of a ship is made to a scale 1: 300
1) The length of the model of the ship is 2 m. Calculate the lengths of the ship.
2) The area of the deck ship is 180,000 m2. Calculate the area of the deck of the model.
3) The volume of the model in 6.5 m3. Calculate the volume of the ship.
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
Find the surface area of a sphere of radius 14 cm.
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved
surface area of the shape if the length of the shape be 7 cm.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate :
- the radius of the solid sphere.
- the number of cones recast. [Take π = 3.14]
What is the least number of solid metallic spheres, each of 6 cm diameter, that should be melted and recast to form a solid metal cone whose height is 45 cm and diameter 12 cm?
Find the total surface area of a hemisphere of radius 10 cm.
The hollow sphere, in which the circus motor cyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding.
The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. Find the height of the cone.
The ratio between the volume of a sphere and volume of a circumscribing right circular cylinder is
Find the volume of a sphere, if its surface area is 154 sq.cm.
Find the radius of a sphere whose surface area is equal to the area of the circle of diameter 2.8 cm
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the weight of the material drilled out if it weighs 7 gm per cm3.
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.
The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹ 0.14 per cm2
