Advertisements
Advertisements
Question
On a map drawn to a scale of 1: 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
1) the actual length of the diagonal distance AC of the plot in km.
2) the actual area of the plot in sq. km.
Solution
Scale: 1:50000
1 cm represents 50000 cm = `50000/(1000xx100)` = 0.5km
1) In ΔABC, by pythagoras theorem
AC2 = AB2 + BC2 = 62 + 82 = 36 + 64 = 100
⇒ AC = 10 cm
⇒ Actual length of diagonal AC = 10 x 0.5 = 5 km
2) 1 cm = 0.5 km
`=> 1 cm^2 = 0.25 km`
Area of rectangle ABCD = AB x BC = 6 x8 = 48 cm2
⇒ Actual area of a plot = 48 x 0.25 = 12 km2
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of diameter 21 cm.
`["Assume "pi=22/7]`
The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface area.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
Find the surface area of a sphere of diameter 3.5 cm .
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
The surface area of a sphere is 2464 cm2, find its volume.
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made?
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere?
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
A hollow sphere of internal and external diameter 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm.
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate :
- the radius of the solid sphere.
- the number of cones recast. [Take π = 3.14]
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
3.5 cm
Find the length of the wire of diameter 4 m that can be drawn from a solid sphere of radius 9 m.
A solid metallic cylinder has a radius of 2 cm and is 45 cm tall. Find the number of metallic spheres of diameter 6 cm that can be made by recasting this cylinder .
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
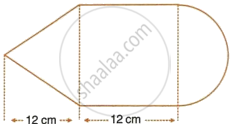
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
The volume of a sphere is 905 1/7 cm3, find its diameter.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
