Advertisements
Advertisements
प्रश्न
On a map drawn to a scale of 1: 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
1) the actual length of the diagonal distance AC of the plot in km.
2) the actual area of the plot in sq. km.
उत्तर
Scale: 1:50000
1 cm represents 50000 cm = `50000/(1000xx100)` = 0.5km
1) In ΔABC, by pythagoras theorem
AC2 = AB2 + BC2 = 62 + 82 = 36 + 64 = 100
⇒ AC = 10 cm
⇒ Actual length of diagonal AC = 10 x 0.5 = 5 km
2) 1 cm = 0.5 km
`=> 1 cm^2 = 0.25 km`
Area of rectangle ABCD = AB x BC = 6 x8 = 48 cm2
⇒ Actual area of a plot = 48 x 0.25 = 12 km2
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of radius 10.5 cm.
`["Assume "pi=22/7]`
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2.
`["Assume "pi=22/7]`
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
Find the surface area of a sphere of radius 5.6 cm .
Find the surface area of a sphere of diameter 14 cm .
Find the volume of a sphere whose surface area is 154 cm2.
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
If the surface area of a sphere is 144π m2, then its volume (in m3) is
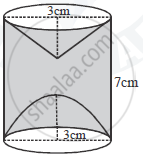
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
If the surface area of a sphere is 2826 cm2 then find its volume. ( π= 3.14)
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the volume of remaining solid
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
Find the volume and surface area of a sphere of diameter 21 cm.
There is a ratio 1: 4 between the surface area of two spheres, find the ratio between their radius.
The radius of a sphere increases by 25%. Find the percentage increase in its surface area
The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹ 0.14 per cm2
The total surface area of a hemisphere is how many times the square of its radius
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
