Advertisements
Advertisements
प्रश्न
The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹ 0.14 per cm2
उत्तर
Internal radius (r) = `20/2` = 10 cm
External radius (R) = `28/2` = 14 cm
T.S.A of a hollow hemisphere
= π (3R2 + r2) sq.units
= `22/7[3 xx 14^2 + 10^2]` cm2
= `22/7[588 + 100]` cm2
= `22/7 xx 688` cm2
Cost of painting the vessel
= `₹ 0.14 xx 22/7 xx 688`
= `₹ 14/100 xx 22/7 xx 688`
= `₹ (2 xx 22 xx 688)/100`
= `₹ 30272/100`
= ₹ 302.72
Cost of painting = ₹ 302.72
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of diameter 3.5 m.
`["Assume "pi=22/7]`
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
Find the surface area of a sphere of diameter 21 cm .
Eight metallic spheres; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
If a solid sphere of radius 10 cm is moulded into 8 spherical solid balls of equal radius, then the surface area of each ball (in sq.cm) is
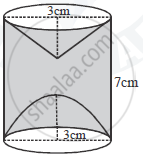
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
Find the radius of a sphere whose surface area is equal to the area of the circle of diameter 2.8 cm
A sphere has the same curved surface area as the curved surface area of a cone of height 36 cm and base radius 15 cm . Find the radius of the sphere .
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
