Advertisements
Advertisements
Question
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
Solution
For sphere, radius = R = 15 cm
For cone, radius = r = 2.5 cm, height, h = 8 cm
Let the number of cones recast be n.
∴ n x Volume of one cone = Volume of solid sphere
`=> n xx 1/3 pir^2h = 4/3piR^3`
`=> n xx (2.5)^2 xx (8) = 4 xx (15)^3`
`=> n = (4 xx 15 xx 15 xx 15)/(2.5 xx 2.5 xx 8)`
`=> n = 270`
Thus, 270 cones were recast.
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of radius 14 cm.
`["Assume "pi=22/7]`
Find the radius of a sphere whose surface area is 154 cm2.
`["Assume "pi=22/7]`
Find the surface area of a sphere of diameter 21 cm .
A hemi-spherical dome of a building needs to be painted. If the circumference of the base of
the dome is 17.6 cm, find the cost of painting it, given the cost of painting is Rs. 5 per l00
`cm^2`
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
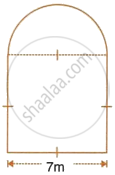
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.
Find the volume of a sphere whose surface area is 154 cm2.
Mark the correct alternative in each of the following:
In a sphere the number of faces is
The ratio of the total surface area of a sphere and a hemisphere of same radius is
If a sphere is inscribed in a cube, then the ratio of the volume of the sphere to the volume of the cube is
A cone and a hemisphere have equal bases and equal volumes the ratio of their heights is
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
9 cm
Find the volume of the hollow sphere whose inner diameter is 8 cm and the thickness of the material of which it is made is 1 cm .
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the weight of the material drilled out if it weighs 7 gm per cm3.
The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
