Advertisements
Advertisements
Question
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.

Solution
Side of square = 7 m
Radius of semicircle = `7/2` m
Length of the tunnel = 80 m
Area of cross-section of the front part = `a^2 + 1/2pir^2`
= `7 xx 7 + 1/2 xx 22/7 xx 7/2 xx 7/2`
= `49 + 77/4 m^2`
= `(196 + 77)/4`
= `273/4 m^2`
i. Therefore, volume of tunnel = area × length
= `273/4 xx 80`
= 5460 m3
ii. Circumference of the front of tunnel
= `2 xx 7 + 1/2 xx 2pir`
= `14 + 22/7 xx 7/2`
= 14 + 11
= 25 m
Therefore, surface area of the inner part of the tunnel
= 25 × 80
= 2000 m2
iii. Area of floor = l × b
= 7 × 80
= 560 m2
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of diameter 3.5 m.
`["Assume "pi=22/7]`
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2.
`["Assume "pi=22/7]`
The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface area.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
Find the surface area of a sphere of radius 14 cm.
Assuming the earth to be a sphere of radius 6370 km, how many square kilo metres is area
of the land, if three-fourth of the earth’s surface is covered by water?
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
Eight metallic spheres; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π, the volume of the solid.
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
If a sphere is inscribed in a cube, find the ratio of the volume of cube to the volume of the sphere.
The ratio between the volume of a sphere and volume of a circumscribing right circular cylinder is
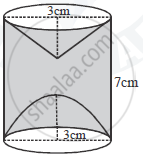
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
3.5 cm
A solid, consisting of a right circular cone standing on a hemisphere, is placed upright, in a right circular cylinder, full of water and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer to the nearest cubic centimetre.
There is surface area and volume of a sphere equal, find the radius of sphere.
There is a ratio 1: 4 between the surface area of two spheres, find the ratio between their radius.
A spherical cannon ball, 28 cm in diameter is melted and recast into a right circular conical mould, the base of which is 35 cm in diameter. Find the height of the cone, correct to one place of decimal.
The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹ 0.14 per cm2
