Advertisements
Advertisements
Question
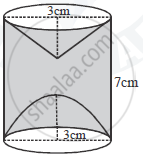
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
Solution
Required volume = Volume of cylinder – Volume of hemisphere – Volume of Cone ...(1)
For cone = Volume `= 1/3 pi r_1^2 h-1`
`= 1/3 xx pi xx(3)^2 xx 3`
`= 9 pi " cm"^3` ...(2)
For Hemisphere = Volume ` = 2/3 pi r _ 2^3 `
` = 2/3 xx pi xx (3)^3`
`= 18 pi " cm"^3 ` ...(3)
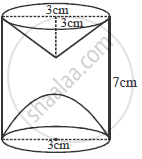
For cylinder = Volume `= pi r _3^2 h _3`
` = pi xx (3)^2 xx 7`
` = 63 pi` ...(4)
∴ Required volume = 63π - 18π - 9π {From (1), (2), (3) and (4)}
= 36 π
`= 36 xx 22/7 " cm"^3`
` = 113.14 " cm"^3`
` = 113 " cm"^3`
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of radius 14 cm.
`["Assume "pi=22/7]`
The surface area of a sphere is 2464 cm2, find its volume.
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere?
The surface area of a solid sphere is increased by 12% without changing its shape. Find the percentage increase in its:
- radius
- volume
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
A hemi-spherical bowl has negligible thickness and the length of its circumference is 198 cm. Find the capacity of the bowl.
Determine the ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube.
The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. Find the height of the cone.
The total surface area of a hemisphere of radius r is
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in meters.
(ii) If the actual volume of a tank at the top of the building is 27m3, find the volume of the tank on the top of the model.
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
9 cm
If the surface area of a sphere is 2826 cm2 then find its volume. ( π= 3.14)
The radius of a sphere is 9 cm. It is melted and drawn into a wire of diameter 2 mm. Find the length of the wire in metre.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate : the number of cones recast. `("Take" pi =22/7)`
There is a ratio 1: 4 between the surface area of two spheres, find the ratio between their radius.
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.
The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratios of the surface areas of the balloon in the two cases is ______.
