Advertisements
Advertisements
Question
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π, the volume of the solid.
Solution
Given, Radius of each cone and hemi-sphere (r) = 8 cm
Height of cone (h) = r = 8 cm
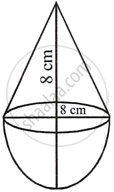
∴ Volume of solid
= `1/3pir^2h + 2/3pir^3`
= `1/3pir^2(h + 2r) cm^3`
= `1/3pi xx 8 xx 8(8 + 2 xx 8) cm^3`
= `64/3 pi(8 + 16) cm^3`
= `64/3pi xx 24`
= 512 π cm3
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of radius 5.6 cm.
`["Assume "pi=22/7]`
The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface area.
A model of a ship is made to a scale 1: 300
1) The length of the model of the ship is 2 m. Calculate the lengths of the ship.
2) The area of the deck ship is 180,000 m2. Calculate the area of the deck of the model.
3) The volume of the model in 6.5 m3. Calculate the volume of the ship.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made?
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm?
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
The largest sphere is cut off from a cube of side 6 cm. The volume of the sphere will be
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is
Find the surface area and volume of sphere of the following radius. (π = 3.14)
4 cm
Find the radius of a sphere whose surface area is equal to the area of the circle of diameter 2.8 cm
Find the radius of the sphere whose surface area is equal to its volume .
Find the volume of the hollow sphere whose inner diameter is 8 cm and the thickness of the material of which it is made is 1 cm .
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the volume of remaining solid
The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹ 0.14 per cm2
The total surface area of a hemisphere is how many times the square of its radius
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
