Advertisements
Advertisements
Question
A solid, consisting of a right circular cone standing on a hemisphere, is placed upright, in a right circular cylinder, full of water and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer to the nearest cubic centimetre.
Solution
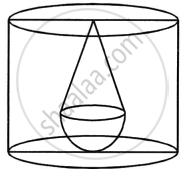
Radius of cylinder = 3 cm
Height of cylinder = 6 cm
Radius of hemisphere = 2 cm
Height of cone = 4 cm
Volume of water in the cylinder when it is full
= πr2h
= π × 3 × 3 × 6
= 54π cm3
Volume of water displaced = Volume of cone + Volume of hemisphere
= `1/3 pir^2h + 2/3 pir^3`
= `1/3 pir^2 (h + 2r)`
= `1/3 pi xx 2 xx 2(4 + 2 xx 2)`
= `1/3 pi xx 4 xx 8`
= `32/3 pi cm^3`
Therefore, volume of water which is left
= `54 pi - 32/3 pi`
= `130/3 pi cm^3`
= `130/3 xx 22/7 cm^3`
= `2860/21 cm^3`
= 136.19 cm3
= 136 cm3
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of diameter 3.5 m.
`["Assume "pi=22/7]`
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.
Find the surface area of a sphere of radius 14 cm.
Assuming the earth to be a sphere of radius 6370 km, how many square kilo metres is area
of the land, if three-fourth of the earth’s surface is covered by water?
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
The surface area of a solid sphere is increased by 12% without changing its shape. Find the percentage increase in its:
- radius
- volume
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
The total surface area of a hemisphere of radius r is
A cylindrical rod whose height is 8 times of its radius is melted and recast into spherical balls of same radius. The number of balls will be
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
Find the radius of the sphere whose surface area is equal to its volume .
Find the volume of the hollow sphere whose inner diameter is 8 cm and the thickness of the material of which it is made is 1 cm .
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate : the number of cones recast. `("Take" pi =22/7)`
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the volume of remaining solid
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones used.
There is a ratio 1: 4 between the surface area of two spheres, find the ratio between their radius.
A spherical cannon ball, 28 cm in diameter is melted and recast into a right circular conical mould, the base of which is 35 cm in diameter. Find the height of the cone, correct to one place of decimal.
The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
