Advertisements
Advertisements
Question
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.
Solution
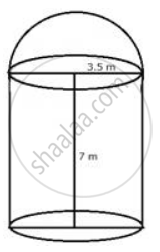
Radius of the cylinder = 3.5 m
Height = 7 m
Total surface area of container excluding the base = Curved
surface area of the cylinder + area of hemisphere
`= 2 pi"rh" + 2pi "r"^2`
`= (2xx22/7 xx 3.5 xx 7) + (2 xx 22/7 xx 3.5 xx 3.5)`
= 154 + 77 m2
= 231 m2
APPEARS IN
RELATED QUESTIONS
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
`["Assume "pi=22/7]`
Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?

A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is `4 2/3` m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter ? Also, find the cost of plastering its inner surface at Rs 4.50 per sq meter.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
A closed cylindrical tank, made of thin ironsheet, has diameter = 8.4 m and height 5.4 m. How much metal sheet, to the nearest m2, is used in making this tank, if `1/15` of the sheet actually used was wasted in making the tank?
Volume of a cylinder with radius h and height r is ______.
The thickness of a hollow metallic cylinder is 2 cm. It is 70 cm long with outer radius of 14 cm. Find the volume of the metal used in making the cylinder, assuming that it is open at both the ends. Also find its weight if the metal weighs 8 g per cm3.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled and the radius is halved.
A housing society consisting of 5,500 people needs 100 L of water per person per day. The cylindrical supply tank is 7 m high and has a diameter 10 m. For how many days will the water in the tank last for the society?
