Advertisements
Advertisements
Question
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is `4 2/3` m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
Solution
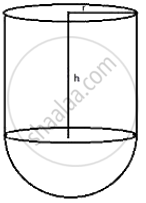
Diameter of the base = 3.5 m
Therefore, radius =`3.5/2 m = 1.75 m = 7/4 m`
Height of cylindrical part = `4 2/3 = 14/3 m `
(i) Capacity (volume) of the vessel
= `pir^2h + 2/3pir^3`
= `pir^2(h + 2/3r)`
= `22/7 xx 7/4 xx 7/4(14/3 + 2/3 xx 7/4)`
= `77/8(14/3 + 7/6)`
= `77/8((28 + 7)/6)`
= `77/8 xx 35/6`
= `2695/48`
= 56.15 m3
(ii) Internal curved surface area
= `2pirh + 2pir^2 = 2pir(h + r) `
= `2 xx 22/7 xx 7/4(14/3 + 7/4)`
= `11((56 + 21)/12)`
= `11 xx 77/12`
= `847/12`
= 70.58 m2
APPEARS IN
RELATED QUESTIONS
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
`["Assume "pi=22/7]`
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small container each of diameter 3 cm and height 4 cm. How many container are necessary to empty the bowl?
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gm of mass (approx). (Take π = `355/113`)
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
The inner radius of a pipe is 2.1 cm. How much water can 12 m of this pipe hold?
Find the volume of the cylinder if the circumference of the cylinder is 132 cm and height is 25 cm.
A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
The ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height is
If the height of a cylinder becomes `1/4` of the original height and the radius is doubled, then which of the following will be true?
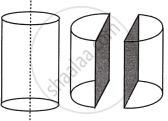
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.