Advertisements
Advertisements
Question
Find the volume of the cylinder if the circumference of the cylinder is 132 cm and height is 25 cm.
Solution
Given: Circumference of the base of cylinder = 132 cm and height h = 25 cm
Circumference of base of cylinder = 2πr
⇒ 132 = 2πr
⇒ 132 = `2 xx 22/7` r
⇒ r = `(132 xx 7)/(2 xx 22)`
⇒ r = `924/44`
⇒ r = 21 cm
Height = 25 cm
Volume = πr2h
= `22/7 xx 21 xx 21 xx 25`
= 22 × 3 × 21 × 25
= 34650 cm3
RELATED QUESTIONS
The circumference of the base of the cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000 cm3 = 1l)
`["Assume "pi=22/7]`
A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.
Water is being pumped out through a circular pipe whose external diameter is 7 cm. If the flow of water is 72 cm per second how many litres of water are being pumped out in one hour.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?
If the radius of a cylinder is doubled and height is halved, the volume will be doubled.
The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kilolitres of water. Water is pumped into the tank to fill to its capacity. Calculate the volume of water pumped into the tank.
Two cylinders of equal volume have heights in the ratio 1 : 9. The ratio of their radii is ______.
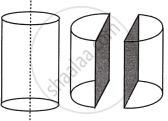
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.