Advertisements
Advertisements
Question
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.
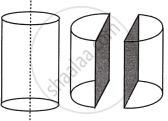
Solution
Here, radius of cylinder (r) = `7/2` cm ...(∴ d = 7 cm)
Height of cylinder = 10 cm
a. T.S.A of a half cylinder
`(πr^2)/2 + (πr^2)/2 + (2πrh)/2 + d xx h`
= `πr^2 + πrh + d xx h`
= `22/7 xx 7/2 xx 7/2 + 22/7 xx 7/2 xx 10 + 7 xx 10`
= `77/2 + 110 + 70`
= `77/2 + 180`
= `(77 + 360)/2`
= `437/2`
= 218.5 cm2
So, total surface area of each half is 218.5 cm2.
b. Cost of painting = Total surface area × Rate of painting
= (218.5 + 218.5) × 30
= ₹ 13,110
APPEARS IN
RELATED QUESTIONS
A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
`["Assume "pi=22/7]`
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small container each of diameter 3 cm and height 4 cm. How many container are necessary to empty the bowl?
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemispherical lid. Find the volume of its interior, including the part covered by the lid.
The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find : the total surface area.
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the area covered by the cylinder in `4 1/2` seconds.
The diameter of the cross-section of a water pipe is 5 cm. Water flows through it at 10km/hr into a cistern in the form of a cylinder. If the radius of the base of the cistern is 2.5 m, find the height to which the water will rise in the cistern in 24 minutes.
A right-angled triangle whose sides are 6 cm, 8 cm and 10 cm is revolved about the sides containing the right angle in two ways. Find the difference in volumes of the two solids so formed.
If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
The dimensions of a godown are 40 m, 25 m and 10 m. If it is filled with cuboidal boxes each of dimensions 2 m × 1.25 m × 1 m, then the number of boxes will be ______.
Two cylinders of equal volume have heights in the ratio 1 : 9. The ratio of their radii is ______.
