Advertisements
Advertisements
Question
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemispherical lid. Find the volume of its interior, including the part covered by the lid.
Solution
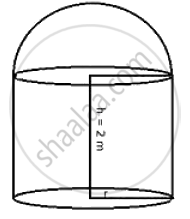
Diameter of cylindrical boiler = 3.5 m
∴ Radius (r) = `3.5/2 = 35/20 = 7/4 m `
Height (h) = 2 m
Radius of hemisphere (R) = `7/4 m `
Total volume of the boiler = `pir^2h + 2/3pir^3`
= `pir^2(h + 2/3r)`
= `22/7 xx 7/7 xx 7/4(2 + 2/3 xx 7/4)`
= `77/8(2 + 7/6)`
= `77/8 xx 19/6`
= `1463/48`
= 30.48 m3
APPEARS IN
RELATED QUESTIONS
Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?

A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
Find the volume of the cylinder if the circumference of the cylinder is 132 cm and height is 25 cm.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their curved surface areas.
Find the weight of a lead pipe 35 cm long. The external diameter of the pipe is 2.4 cm and the thickness of the pipe is 2mm, given 1 cm3 of lead weighs 10 gm.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is
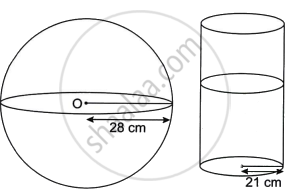
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`