Advertisements
Advertisements
Question
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
Solution
Let the height by which the water ups be = h cm
Volume of the increase in water = 3.142 x 10 x 10 x h cm3
Volume of the cube = 8 x 8 x 8 cm3
Both the above volumes are equal
∴ 3.142 x 10 x 10 x h = 8 x 8 x 8
h = `(8 xx 8 xx 8)/(3.142 xx 10 xx 10) = 1.6` cm
The height h = 16 mm.
APPEARS IN
RELATED QUESTIONS
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s–1. Calculate, in minutes, the time it takes to fill the tank.
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter ? Also, find the cost of plastering its inner surface at Rs 4.50 per sq meter.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
The radius and height of a cylinder are in the ratio of 5 : 7 and its volume is 550 cm. Find its radius. (Take π = 22/7)
30 circular plates, each of radius 14 cm and thickness 3 cm are placed one above the another to form a cylindrical solid. Find volume of the cylinder so formed.
The dimensions of a godown are 40 m, 25 m and 10 m. If it is filled with cuboidal boxes each of dimensions 2 m × 1.25 m × 1 m, then the number of boxes will be ______.
The ratio of radii of two cylinders is 1 : 2 and heights are in the ratio 2 : 3. The ratio of their volumes is ______.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height remains same and the radius is halved.
A hollow garden roller of 42 cm diameter and length 152 cm is made of cast iron 2 cm thick. Find the volume of iron used in the roller.
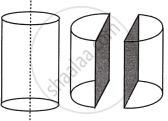
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.