Advertisements
Advertisements
प्रश्न
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemispherical lid. Find the volume of its interior, including the part covered by the lid.
उत्तर
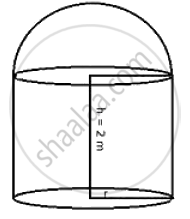
Diameter of cylindrical boiler = 3.5 m
∴ Radius (r) = `3.5/2 = 35/20 = 7/4 m `
Height (h) = 2 m
Radius of hemisphere (R) = `7/4 m `
Total volume of the boiler = `pir^2h + 2/3pir^3`
= `pir^2(h + 2/3r)`
= `22/7 xx 7/7 xx 7/4(2 + 2/3 xx 7/4)`
= `77/8(2 + 7/6)`
= `77/8 xx 19/6`
= `1463/48`
= 30.48 m3
APPEARS IN
संबंधित प्रश्न
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
`["Assume "pi=22/7]`
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find the volume of the cylinder correct to one decimal place.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find :
- radius of the vessel.
- height of the vessel.
- wetted surface area of the vessel when it is half-filled with water.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their curved surface areas.
A closed cylindrical tank, made of thin ironsheet, has diameter = 8.4 m and height 5.4 m. How much metal sheet, to the nearest m2, is used in making this tank, if `1/15` of the sheet actually used was wasted in making the tank?
The ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height is
The volume of the largest right circular cone that can be fitted in a cube whose edge is 2r equals to the volume of a hemisphere of radius r.
A school provides milk to the students daily in a cylindrical glasses of diameter 7 cm. If the glass is filled with milk upto an height of 12 cm, find how many litres of milk is needed to serve 1600 students.
30 circular plates, each of radius 14 cm and thickness 3 cm are placed one above the another to form a cylindrical solid. Find volume of the cylinder so formed.
From a pipe of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in 1 hour.
