Question

A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate :

1. total surface area of the tent,
2. area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.

Answer 1

 
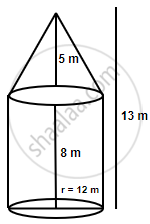
Height of the cylindrical part = H = 8 m

Height of the conical part = h = (13 – 8) m = 5 m

Diameter = 24 m ⟶ radius = r = 12 m  

Slant height of the cone = l 

`l = sqrt(r^2 + h^2)` 

`l = sqrt(12^2 + 5^2)` 

`l = sqrt(169) = 13  m` 

Slant height of cone = 13 m 

i. Total surface are of the tent

= 2πrh + πrl

= πr(2h + l) 

= `22/7 xx 12 xx (2 xx 8 + 13)` 

= `264/7(16 + 13)`

= `264/7 xx 29` 

= `7656/7 m^2` 

= 1093.71 m² 

ii. Area of canvas used in stitching = Total area 

Total area of canvas = `7656/7 + "Total area of canvas"/10` 

`=>` Total area of canvas – `"Total area of canvas"/10 = 7656/7` 

`=> "Total area of canvas" (1 - 1/10) = 7656/7` 

`=> "Total area of canvas" xx 9/10 = 7656/7`  

`=>` Total area of canvas = `7656/7 xx 10/9` 

`=>` Total area of canvas = `76560/63 = 1215.23  m^2`