Advertisements
Advertisements
Question
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate :
- total surface area of the tent,
- area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
Solution
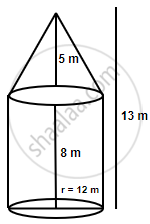
Height of the cylindrical part = H = 8 m
Height of the conical part = h = (13 – 8) m = 5 m
Diameter = 24 m ⟶ radius = r = 12 m
Slant height of the cone = l
`l = sqrt(r^2 + h^2)`
`l = sqrt(12^2 + 5^2)`
`l = sqrt(169) = 13 m`
Slant height of cone = 13 m
i. Total surface are of the tent
= 2πrh + πrl
= πr(2h + l)
= `22/7 xx 12 xx (2 xx 8 + 13)`
= `264/7(16 + 13)`
= `264/7 xx 29`
= `7656/7 m^2`
= 1093.71 m2
ii. Area of canvas used in stitching = Total area
Total area of canvas = `7656/7 + "Total area of canvas"/10`
`=>` Total area of canvas – `"Total area of canvas"/10 = 7656/7`
`=> "Total area of canvas" (1 - 1/10) = 7656/7`
`=> "Total area of canvas" xx 9/10 = 7656/7`
`=>` Total area of canvas = `7656/7 xx 10/9`
`=>` Total area of canvas = `76560/63 = 1215.23 m^2`
APPEARS IN
RELATED QUESTIONS
It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
`["Assume "pi=22/7]`
Find the volume of the cylinder if the height (h) and radius of the base (r) are as given below.
r = 10.5 cm, h = 8 cm
How much iron is needed to make a rod of length 90 cm and diameter 1.4 cm?
Two-cylinder have bases of the same size. The diameter of each is 14 cm. One of the cones is 10 cm high and the other is 20 cm high. Find the ratio between their volumes.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
Find the number of coins, 1.5 cm in diameter and 2 mm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm
Two cylinders of equal volume have heights in the ratio 1 : 9. The ratio of their radii is ______.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height remains same and the radius is halved.
A rectangular sheet of paper is rolled in two different ways to form two different cylinders. Find the volume of cylinders in each case if the sheet measures 44 cm × 33 cm.
Volume of a cylinder of height 3 cm is a 48π. Radius of the cylinder is ______.
