Advertisements
Advertisements
प्रश्न
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled and the radius is halved.
उत्तर
∵ Volume of a cylinder = πr2h
Where, h is height and r is radius of base of the cylinder.
If height is doubled and the radius is halved,
i.e. h = 2h and `r = r/2`
∴ Volume = `pi xx (r/2) xx (r/2) xx 2h`
= `pi xx r^2/4 xx 2h`
= `(pir^2h)/2`
Hence, volume became half of the original volume.
APPEARS IN
संबंधित प्रश्न
The circumference of the base of the cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000 cm3 = 1l)
`["Assume "pi=22/7]`
It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
`["Assume "pi=22/7]`
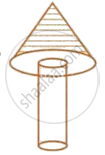
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
The height and the radius of the base of a cylinder are in the ratio 3 : 1. If it volume is 1029 π cm3; find it total surface area.
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find the volume of the cylinder correct to one decimal place.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its :
- shorter side.
- longer side.
Two solid cylinders, one with diameter 60 cm and height 30 cm and the other with radius 30 cm and height 60 cm, are metled and recasted into a third solid cylinder of height 10 cm. Find the diameter of the cylinder formed.
Two-cylinder have bases of the same size. The diameter of each is 14 cm. One of the cones is 10 cm high and the other is 20 cm high. Find the ratio between their volumes.
If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
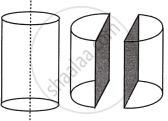
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.