Advertisements
Advertisements
प्रश्न
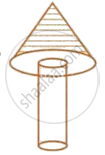
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
उत्तर
Height of the cone = 24 cm
Height of the cylinder = 36 cm
Radius of the cone = twice the radius of the cylinder = 10 cm
Radius of the cylinder = 5 cm
Slant height of the cone = `sqrt(r^2 + h^2)`
= `sqrt(10^2 + 24^2)`
= `sqrt(100 + 576)`
= `sqrt(676)`
= 26 cm
Now, the surface area of the toy = curved area of the conical point + curved area of the cylinder
= πrl + πr2 + 2πRH
= π[rl + r2 + 2RH]
= 3.14[10 × 26 × (10)2 + 2 × 5 × 36]
= 3.14[260 + 100 + 360]
= 3.14[720]
= 2260.8 cm2
APPEARS IN
संबंधित प्रश्न
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is `4 2/3` m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is `5159/6 cm^3` and `4235/6 cm^3` of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter? Also, find the cost of plastering its inner surface at Rs. 4.50 per sq.meter.
A cylinderical container with a diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimesions 22 cm × 14 cm × 10.5 cm. Find the rise in level of the water when the solid is submerged.
The total surface area of a solid cylinder is 616 cm2. If the ratio between its curved surface area and total surface area is 1 : 2; find the volume of the cylinder.
A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?
The volume of the largest right circular cone that can be fitted in a cube whose edge is 2r equals to the volume of a hemisphere of radius r.
The ratio of radii of two cylinders is 1 : 2 and heights are in the ratio 2 : 3. The ratio of their volumes is ______.
The volume of a cylinder which exactly fits in a cube of side a is ______.
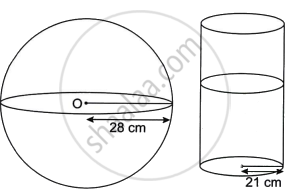
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`