Advertisements
Advertisements
प्रश्न
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is `4 2/3` m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
उत्तर
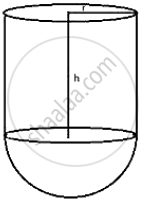
Diameter of the base = 3.5 m
Therefore, radius =`3.5/2 m = 1.75 m = 7/4 m`
Height of cylindrical part = `4 2/3 = 14/3 m `
(i) Capacity (volume) of the vessel
= `pir^2h + 2/3pir^3`
= `pir^2(h + 2/3r)`
= `22/7 xx 7/4 xx 7/4(14/3 + 2/3 xx 7/4)`
= `77/8(14/3 + 7/6)`
= `77/8((28 + 7)/6)`
= `77/8 xx 35/6`
= `2695/48`
= 56.15 m3
(ii) Internal curved surface area
= `2pirh + 2pir^2 = 2pir(h + r) `
= `2 xx 22/7 xx 7/4(14/3 + 7/4)`
= `11((56 + 21)/12)`
= `11 xx 77/12`
= `847/12`
= 70.58 m2
APPEARS IN
संबंधित प्रश्न
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s–1. Calculate, in minutes, the time it takes to fill the tank.
What length of solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of external diameter 20 cm, 0.25 cm thick and 15 cm long?
A cylinderical container with a diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimesions 22 cm × 14 cm × 10.5 cm. Find the rise in level of the water when the solid is submerged.
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the area covered by the cylinder in `4 1/2` seconds.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its :
- shorter side.
- longer side.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their volumes.
Two-cylinder have bases of the same size. The diameter of each is 14 cm. One of the cones is 10 cm high and the other is 20 cm high. Find the ratio between their volumes.
From a pipe of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in 1 hour.
