Advertisements
Advertisements
प्रश्न
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is `5159/6 cm^3` and `4235/6 cm^3` of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
उत्तर
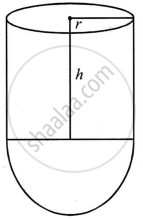
Volume of water filled in the test tube =`5159/6 cm^3`
Volume of water filled up to 4 cm =`4235/6 cm^3`
Let r be the radius and h be the height of test tube
∴ `2/3 pir^3 + pir^2h = 5159/6`
`=> pir^2(2/3r + h) = 5159/6`
`=> (pir^2)/3(2r + 3h) = 5159/6`
`=> pir^2(2r + 3h) = 5159/2` ...(i)
And
`2/3pir^3 + pir^2(h - 4) = 4235/6`
`=> pir^2(2/3r + h - 4) = 4235/6`
`=> (pir^2)/3(2r + 3h - 12) = 4235/6`
`=> pir^2(2r + 3h - 12) = 4235/2` ...(ii)
Dividing (i) by (ii)
`(2r + 3h)/(2r + 3h - 12) = 5259/4235` ...(iii)
Subtracting (ii) from (i)
`pir^2(12) = 5159/2 - 4235/2 = 924/2`
`=> 12 xx 22/7 xx r^2 = 924/2`
`=> r^2 = (924 xx 7)/(2 xx 12 xx 22) = (7 xx 7)/(2 xx 2)`
`=> r^2 = 49/4`
`=> r = 7/2 = 3.5 cm`
Subtracting the value of r in (iii)
`(2 xx 7/2 + 3h)/(2 xx 7/2 + 3h - 12) = 5159/4235`
`=> (7 + 3h)/(7 + 3h - 12) = 5159/4235`
`=> (7 + 3h)/(7 + 3h - 12) = 469/385`
`=>` 2695 + 1155h = 1407h – 2345
`=>` 252h = 5040
`=>` h = 20
Hence, height = 20 cm and radius = 3.5 cm
APPEARS IN
संबंधित प्रश्न
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find (i) radius of its base (ii) its volume. [Use π = 3.14]
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed. Find the volume of the remaining solid.
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm × 14 cm × 10.5 cm. Find the rise in the level of the water when the solid is submerged.
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find the height of the cylinder correct to one decimal place.
The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find : the total surface area.
The total surface area of a hollow cylinder, which is open from both the sides, is 3575 cm2; area of its base ring is 357.5 cm2 and its height is 14 cm. Find the thickness of the cylinder.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?
30 circular plates, each of radius 14 cm and thickness 3 cm are placed one above the another to form a cylindrical solid. Find volume of the cylinder so formed.
