Advertisements
Advertisements
Question
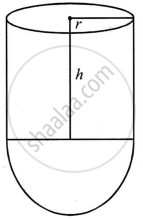
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is `5159/6 cm^3` and `4235/6 cm^3` of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
Solution
Volume of water filled in the test tube =`5159/6 cm^3`
Volume of water filled up to 4 cm =`4235/6 cm^3`
Let r be the radius and h be the height of test tube
∴ `2/3 pir^3 + pir^2h = 5159/6`
`=> pir^2(2/3r + h) = 5159/6`
`=> (pir^2)/3(2r + 3h) = 5159/6`
`=> pir^2(2r + 3h) = 5159/2` ...(i)
And
`2/3pir^3 + pir^2(h - 4) = 4235/6`
`=> pir^2(2/3r + h - 4) = 4235/6`
`=> (pir^2)/3(2r + 3h - 12) = 4235/6`
`=> pir^2(2r + 3h - 12) = 4235/2` ...(ii)
Dividing (i) by (ii)
`(2r + 3h)/(2r + 3h - 12) = 5259/4235` ...(iii)
Subtracting (ii) from (i)
`pir^2(12) = 5159/2 - 4235/2 = 924/2`
`=> 12 xx 22/7 xx r^2 = 924/2`
`=> r^2 = (924 xx 7)/(2 xx 12 xx 22) = (7 xx 7)/(2 xx 2)`
`=> r^2 = 49/4`
`=> r = 7/2 = 3.5 cm`
Subtracting the value of r in (iii)
`(2 xx 7/2 + 3h)/(2 xx 7/2 + 3h - 12) = 5159/4235`
`=> (7 + 3h)/(7 + 3h - 12) = 5159/4235`
`=> (7 + 3h)/(7 + 3h - 12) = 469/385`
`=>` 2695 + 1155h = 1407h – 2345
`=>` 252h = 5040
`=>` h = 20
Hence, height = 20 cm and radius = 3.5 cm
APPEARS IN
RELATED QUESTIONS
The circumference of the base of the cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000 cm3 = 1l)
`["Assume "pi=22/7]`
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
`["Assume "pi=22/7]`
Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
- To find how much it can hold
- Number of cement bags required to plaster it
- To find the number of smaller tanks that can be filled with water from it.
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of dimensions 7.5 m by 5 m by 4 m; calculate the rise in level in the cistern in 1 hour 15 minutes.
How much iron is needed to make a rod of length 90 cm and diameter 1.4 cm?
Two-cylinder have bases of the same size. The diameter of each is 14 cm. One of the cones is 10 cm high and the other is 20 cm high. Find the ratio between their volumes.
If the circumference of a conical wooden piece is 484 cm then find its volume when its height is 105 cm.
A small village, having a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?
The volume of a cylinder which exactly fits in a cube of side a is ______.
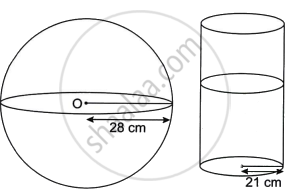
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`