Advertisements
Advertisements
Question
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and height of the cylindrical part of 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m2.
Solution 1
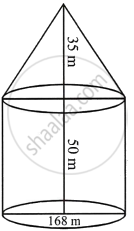
Total height of the tent = 85 m
Diameter of the base = 168 m
Therefore, radius (r) = 84 m
Height of the cylindrical part = 50 m
Then height of the conical part = (85 – 50) = 35 m
Slant height (l) = `sqrt(r^2 + h^2)`
= `sqrt(84^2 + 35^2)`
= `sqrt(7056 + 1225)`
= `sqrt(8281)`
= 91 cm
Total surface area of the tent = 2πrh + πrl
= π(2h + l)
= `22/7 xx 84(2 xx 50 + 91)`
= 264(100 + 91)
= 264 × 191
= 50424 m2
Since 20% extra is needed for folds and stitching,
total area of canvas needed
= `50424 xx 120/100`
= 60508.8
= 60509 m2
Solution 2

∴ Radius of box = `168/2` = 84 m
Height of the cone = 35 m
Height of cylinder = 50 m
Curved surface of the tent
= 2πrh + πrl
= `2 xx 22/7 xx 84 xx 50 + 22/7 xx 84 xx 91` ...(l2 = 352 + 842 i.e., l = 91)
= 44 × 12 × 50 + 22 × 12 × 91
= 26,400 + 24,024
= 50,424 sq.m.
Area of the canvas required with (20% extra)
= `120/100 xx 50,424 `
= 60,508.8 sq.m.
= 60,509 m2
RELATED QUESTIONS
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
`["Assume "pi=22/7]`
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find (i) radius of its base (ii) its volume. [Use π = 3.14]
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at Rs. 15 per metre if the width is 1.5 m.
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is `3 1/2` cm and height 8 cm. Find the volume of water required to fill the vessel. If this cone is replaced by another cone, whose height is `1 3/4` cm and the radius of whose base is 2 cm, find the drop in the water level.
Find the total surface area of an open pipe of length 50 cm, external diameter 20 cm and internal diameter 6 cm.
Water is being pumped out through a circular pipe whose external diameter is 7 cm. If the flow of water is 72 cm per second how many litres of water are being pumped out in one hour.
Find the weight of a lead pipe 35 cm long. The external diameter of the pipe is 2.4 cm and the thickness of the pipe is 2mm, given 1 cm3 of lead weighs 10 gm.
Water flows through a cylindrical pipe of internal diameter 7 cm at 36 km/hr. Calculate the time in minutes it would take to fill the cylindrical tank, the radius of whose base is 35 cm, and height is 1 m.
Volume of a cylinder with radius h and height r is ______.
