Question

An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and height of the cylindrical part of 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m².

Answer 1

 
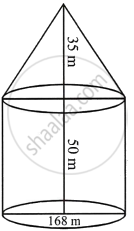
Total height of the tent = 85 m

Diameter of the base = 168 m

Therefore, radius (r) = 84 m

Height of the cylindrical part = 50 m

Then height of the conical part = (85 – 50) = 35 m  

Slant height (l) = `sqrt(r^2 + h^2)`

= `sqrt(84^2 + 35^2)`

= `sqrt(7056 + 1225)`

= `sqrt(8281)`

= 91 cm 

Total surface area of the tent = 2πrh + πrl

= π(2h + l) 

= `22/7 xx 84(2 xx 50 + 91)` 

= 264(100 + 91)

= 264 × 191 

= 50424 m²

Since 20% extra is needed for folds and stitching,
total area of canvas needed 

= `50424 xx 120/100` 

= 60508.8

= 60509 m²  

Answer 2

∴ Radius of box = `168/2` = 84 m

Height of the cone = 35 m

Height of cylinder = 50 m

Curved surface of the tent

= 2πrh + πrl

= `2 xx 22/7 xx 84 xx 50 + 22/7 xx 84 xx 91`  ...(l² = 35² + 84² i.e., l = 91)

= 44 × 12 × 50 + 22 × 12 × 91

= 26,400 + 24,024

= 50,424 sq.m.

Area of the canvas required with (20% extra)

= `120/100 xx 50,424 `

= 60,508.8 sq.m.

= 60,509 m²