Advertisements
Advertisements
प्रश्न
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and height of the cylindrical part of 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m2.
उत्तर १
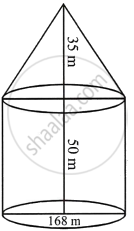
Total height of the tent = 85 m
Diameter of the base = 168 m
Therefore, radius (r) = 84 m
Height of the cylindrical part = 50 m
Then height of the conical part = (85 – 50) = 35 m
Slant height (l) = `sqrt(r^2 + h^2)`
= `sqrt(84^2 + 35^2)`
= `sqrt(7056 + 1225)`
= `sqrt(8281)`
= 91 cm
Total surface area of the tent = 2πrh + πrl
= π(2h + l)
= `22/7 xx 84(2 xx 50 + 91)`
= 264(100 + 91)
= 264 × 191
= 50424 m2
Since 20% extra is needed for folds and stitching,
total area of canvas needed
= `50424 xx 120/100`
= 60508.8
= 60509 m2
उत्तर २

∴ Radius of box = `168/2` = 84 m
Height of the cone = 35 m
Height of cylinder = 50 m
Curved surface of the tent
= 2πrh + πrl
= `2 xx 22/7 xx 84 xx 50 + 22/7 xx 84 xx 91` ...(l2 = 352 + 842 i.e., l = 91)
= 44 × 12 × 50 + 22 × 12 × 91
= 26,400 + 24,024
= 50,424 sq.m.
Area of the canvas required with (20% extra)
= `120/100 xx 50,424 `
= 60,508.8 sq.m.
= 60,509 m2
संबंधित प्रश्न
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
`["Assume "pi=22/7]`
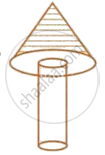
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
The height and the radius of the base of a cylinder are in the ratio 3 : 1. If it volume is 1029 π cm3; find it total surface area.
A solid metallic sphere of radius 6 cm is melted and made into a solid cylinder of height 32 cm. Find the:
(i) radius of the cylinder
(ii) curved surface area of the cylinder
Take π = 3.1
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the area covered by the cylinder in `4 1/2` seconds.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find :
- radius of the vessel.
- height of the vessel.
- wetted surface area of the vessel when it is half-filled with water.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their curved surface areas.
The ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height is
A small village, having a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?
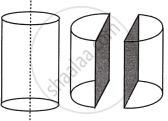
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.