ICSE solutions for Mathematics [English] Class 10 chapter 17 - Mensuration [Latest edition]

Find the area of a circle whose circumference is 22 cm.

If the perimeter of a semi-circular protractor is 36 cm. Find its diameter.

A well 28.8 m deep and of diameter 2 m is dug up. The soil dug out is spread all around the well to make a platform 1 m high considering the fact losse soil settled to a height in the ratio 6 : 5 find the width of the platform.

Two-cylinder have bases of the same size. The diameter of each is 14 cm. One of the cones is 10 cm high and the other is 20 cm high. Find the ratio between their volumes.

A glass cylinder with a diameter 20 cm water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder. (Take π = 3.142)

Water is being pumped out through a circular pipe whose external diameter is 7 cm. If the flow of water is 72 cm per second how many litres of water are being pumped out in one hour.

The diameter of a garden roller is 1.4 m and it is 2 m long. How much area will it cover in 5 revolutions? (Take π = 22/7)

The radius and height of a cylinder are in the ratio of 5 : 7 and its volume is 550 cm. Find its radius. (Take π = 22/7)

The ratio of the base area and the curved surface of a conical tent is 40: 41. If the height is 18 m, Find the air capacity of the tent in terms of n.

The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas. 

The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm³. What is its radius? What is its slant height? (Take π = 3.14)

Find the volume and surface area of a sphere of diameter 21 cm.

The volume of a sphere is 905 1/7 cm³, find its diameter.

There is surface area and volume of a sphere equal, find the radius of sphere.

There is a ratio 1: 4 between the surface area of two spheres, find the ratio between their radius.

Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm, containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.

A spherical cannon ball, 28 cm in diameter is melted and recast into a right circular conical mould, the base of which is 35 cm in diameter. Find the height of the cone, correct to one place of decimal.

A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.

A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast. 

The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.

A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.

A sphere cut out from a side of 7 cm cubes. Find the volume of this sphere?

How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?

A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone.

The total surface area of a hollow metal cylinder, open at both ends of external radius 8 cm and height 10 cm is 338π cm². Taking r to be inner radius, write down an equation in r and use it to state the thickness of the metal in the cylinder.

Find the weight of a lead pipe 35 cm long. The external diameter of the pipe is 2.4 cm and the thickness of the pipe is 2mm, given 1 cm³ of lead weighs 10 gm.

A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)

A road roller is cylindrical in shape, its circular end has a diameter of 1.4 m and its width is 4 m. It is used to level a play ground measuring 70 m × 40 m. Find the minimum number of complete revolutions that the roller must take in order to cover the entire ground once.

A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.

The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)

In the equilateral Δ ABC of side 14 cm, side BC is the diameter of a semicircle as shown in the figure below. Find the area of the shaded region. (Take π = 22/7 and √3 = 1.732)

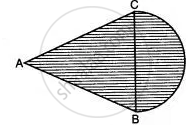
ABC is an isosceles right-angled triangle with ∠ABC = 90°. A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. [Take π = 22/7]

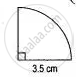
In the adjoining figure, the radius is 3.5 cm. Find:
(i) The area of the quarter of the circle correct to one decimal place.
(ii) The perimeter of the quarter of the circle correct to one decimal place. ( Take π = `22/7`)

The boundary of the shaded region in the given diagram consists of three semicircular areas, the smaller ones being equal and it’s diameter 5 cm, if the diameter of the larger one is 10 cm,
calculate:
(i) The length of the boundary,
(ii) The area of the shaded region.     (Take π = 3.14)

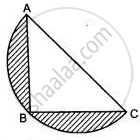
In the given figure, AB is the diameter of a circle with center O and OA = 7 cm. Find the area of the shaded region.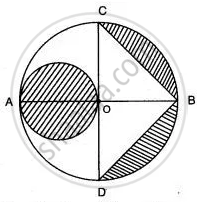

Find the perimeter and area of the shaded portion of the following diagram; give your answer correct to 3 significant figures. (Take π = 22/7).

In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.

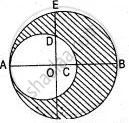
In the given figure, find the area of the unshaded portion within the rectangle. (Take π = 22/7).

The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.

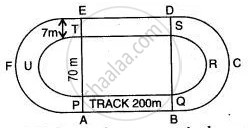
(i) Calculate the area of the grassed enclosure in m².
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)

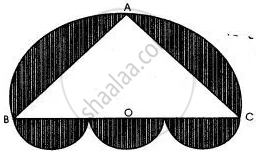
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)

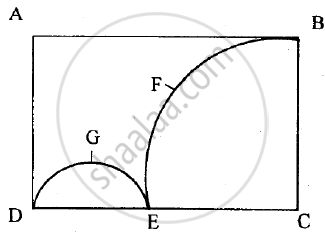
In the figure given below, ABCD is the rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle. (Take `pi = 22/7`).

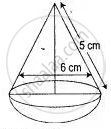
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.

Calculate the area of the shaded region, if the diameter of the semi-circle is equal to 14 cm. (Take π = 22/7).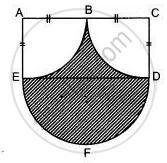

A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.

A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the internal volume of the container in m³.

A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket. (Take π =22/7)

The radius of two right circular cylinder are in the ratio of 2 : 3 and their heights are in the ratio of 5: 4 calculate the ratio of their curved surface areas and also the ratio of their volumes.

A vessel in the form of an inverted cone is filled with water to the brim: Its height is 20 cm and the diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged?

Water flows at the rate of 10 m per minute through a cylindrical pipe 5 mm of diameter. How much time would it take to fill a conical vessel whose diameter at he surface is 40 cm and depth is 24 cm?

A conical tent is accommodate to 11 persons each person must have 4 sq. metre of the space on the ground and 20 cubic metre of air to breath. Find the height of the cone.

A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m calculate the length of the canvas which is 5m wide to make the required tent.

An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and height of the cylindrical part of 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m².

The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?

The cylinder of radius 12 cm have filled the 20 cm with water. One piece of iron drop in the stands of water goes up 6.75 cm. Find the radius of sphere piece.

The radius of the internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm respectively! If it is melted and recast into a solid cylinder of height `8/3` cm, find the diameter of the cylinder.

The surface area of a solid metallic sphere is 616 cm². It is melted and recast into smaller spheres of diameter 3.5 cm. How many such spheres can be obtained?

The diameter of the cross-section of a water pipe is 5 cm. Water flows through it at 10km/hr into a cistern in the form of a cylinder. If the radius of the base of the cistern is 2.5 m, find the height to which the water will rise in the cistern in 24 minutes.

A metallic cylinder has a radius of 3 cm and a height of 5 cm. It is made of metal A. To reduce its weight, a conical hole is drilled in the cylinder, as shown and it is completely filled with a lighter metal B. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of the metal A to the volume of metal B in the solid.

An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.

A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.

A buoy is made in the form of a hemisphere surmounted by a right circular cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 m and its volume is two-third the volume of hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two decimal places. 

Water flows through a cylindrical pipe of internal diameter 7 cm at 36 km/hr. Calculate the time in minutes it would take to fill the cylindrical tank, the radius of whose base is 35 cm, and height is 1 m.