Advertisements
Advertisements
प्रश्न
In the equilateral Δ ABC of side 14 cm, side BC is the diameter of a semicircle as shown in the figure below. Find the area of the shaded region. (Take π = 22/7 and √3 = 1.732)
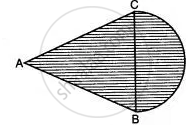
उत्तर
Area of shaded part = Area of equilateral Δ ABC + Area of semicircle
= `sqrt3/4 a^2 + 1/2` πr2
Given a = 14 cm and r = `14/2` = 7 cm
∴ Area of shaded part = `sqrt3/4 xx 14^2 + 1/2 xx 22/7 xx 7 xx 7`
= `(1.732 xx 14 xx 14)/4 + 11 xx 7`
= 1.732 x 7 x 7 + 77
= 84.868 + 77
= 161.868 sq.cm.
APPEARS IN
संबंधित प्रश्न
500 persons have to dip in a rectangular tank which is 80m long and 50m broad. What is the rise in the level of water in the tank, if the average displacement of water by a person is 0.04m3 .
The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed (Use it =`22/7`)
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
The heights of two circular cylinders of equal volume are in the ratio 1 : 2. The ratio of their radii is
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
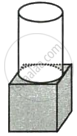
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
A piece of paper is in the shape of a semi-circular region of radius 10 cm. It is rolled to form a right circular cone. The slant height is ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
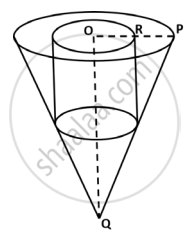
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is ______.
