Advertisements
Advertisements
प्रश्न
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is ______.
पर्याय
48 cm2
72 cm2
96 cm2
108 cm2
उत्तर
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is `underline(bb(96 cm^2)`.
Explanation:
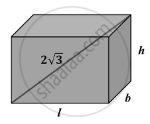
Let Length = l
Breadth = b
Height = h
Given that
Sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm
l + b + h = `6sqrt(3)` cm ......(1)
Also, given that
Length of its diagonal is `2sqrt(3)` cm
`sqrt(l^2 + b^2 + h^2) = 2sqrt(3)` ......(2)
We need to find
Total surface area of the cuboid
Now, Total surface area of cuboid = 2(lb + bh + lh)
From (1)
l + b + h = `6sqrt(3)` cm
Squaring both sides
(l + b + h)2 = `(6sqrt(3))^2`
l2 + b2 + h2 + 2lb + 2bh + 2lh = `6^2 xx (sqrt(3))^2`
l2 + b2 + h2 + 2lb + 2bh + 2lh = 36 × 3
l2 + b2 + h2 + 2lb + 2bh + 2lh = 108
From (1)
`sqrt(l^2 + b^2 + h^2) = 2sqrt(3)`
Squaring both sides
`(sqrt(l^2 + b^2 + h^2))^2 = (2sqrt(3))^2`
l2 + b2 + h2 = 22 × `(sqrt(3))^2`
l2 + b2 + h2 = 4 × 3
l2 + b2 + h2 = 12
12 + 2lb + 2bh + 2lh = 108
2lb + 2bh + 2lh = 108 – 12
2lb + 2bh + 2lh = 96
Total surface area = 96 cm2
APPEARS IN
संबंधित प्रश्न
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm. Use [π = `22/7`]
A bucket made up of a metal sheet is in form of a frustum of cone of height 16cm with diameters of its lower and upper ends as 16cm and 40cm. find the volume of bucket. Also find cost of bucket if the cost of metal sheet used is Rs 20 per 100 cm2
The radii of internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm, respectively. It is melted and recast into a solid cylinder of diameter 14 cm. Find the height of the cylinder.
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
The ratio of the volumes of two spheres is 8 : 27. If r and R are the radii of spheres respectively, then (R – r) : r is ______.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that `1/8` space of the cube remains unfilled. Then the number of marbles that the cube can accomodate is ______.
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
