Advertisements
Advertisements
Question
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is ______.
Options
48 cm2
72 cm2
96 cm2
108 cm2
Solution
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is `underline(bb(96 cm^2)`.
Explanation:
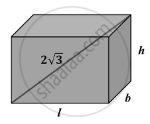
Let Length = l
Breadth = b
Height = h
Given that
Sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm
l + b + h = `6sqrt(3)` cm ......(1)
Also, given that
Length of its diagonal is `2sqrt(3)` cm
`sqrt(l^2 + b^2 + h^2) = 2sqrt(3)` ......(2)
We need to find
Total surface area of the cuboid
Now, Total surface area of cuboid = 2(lb + bh + lh)
From (1)
l + b + h = `6sqrt(3)` cm
Squaring both sides
(l + b + h)2 = `(6sqrt(3))^2`
l2 + b2 + h2 + 2lb + 2bh + 2lh = `6^2 xx (sqrt(3))^2`
l2 + b2 + h2 + 2lb + 2bh + 2lh = 36 × 3
l2 + b2 + h2 + 2lb + 2bh + 2lh = 108
From (1)
`sqrt(l^2 + b^2 + h^2) = 2sqrt(3)`
Squaring both sides
`(sqrt(l^2 + b^2 + h^2))^2 = (2sqrt(3))^2`
l2 + b2 + h2 = 22 × `(sqrt(3))^2`
l2 + b2 + h2 = 4 × 3
l2 + b2 + h2 = 12
12 + 2lb + 2bh + 2lh = 108
2lb + 2bh + 2lh = 108 – 12
2lb + 2bh + 2lh = 96
Total surface area = 96 cm2
APPEARS IN
RELATED QUESTIONS
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.) [use `pi = 22/7`]
A hollow sphere of internal and external diameter 4cm and 8cm is melted into a cone of base diameter 8cm. Calculate height of cone?
A cylindrical road roller made of iron is 1 m long, Its internal diameter is 54 cm and the thickness of the iron sheet used in making the roller is 9 cm. Find the mass of the roller, if 1 cm3 of iron has 7.8 gm mass. (Use π = 3.14)
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
A metallic right circular cone 20cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to base. If frustum so obtained bee
drawn into a wire of diameter
(1/16) cm find length of the wire?
A solid consists of a circular cylinder surmounted by a right circular cone. The height of the cone is h. If the total height of the solid is 3 times the volume of the cone, then the height of the cylinder is
From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.
A hollow sphere of external and internal diameters 8 cm and 4 cm, respectively is melted into a solid cone of base diameter 8 cm. Find the height of the cone.
The diameter of the base of a cone is 42 cm and its volume is 12936 cm3. Its height is
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
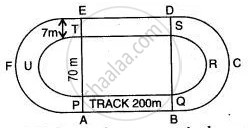
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
