Advertisements
Advertisements
Question
A hollow sphere of internal and external diameter 4cm and 8cm is melted into a cone of base diameter 8cm. Calculate height of cone?
Solution
Given
Internal diameter of hollow sphere (r) = 4cm
So, the internal radius of hollow sphere = 2 cm
External diameter (R) = 8cm
So, the external radius of hollow sphere = 4 cm
Volumeof hollow sphere = `4/3pi(R^2-r^2)`
`=4/3pi(4^2 - 2^2)` ...(1)
Given diameter of cone = 8cm
Radius of cone = 4cm
Let height of cone be x cm
Volume of cone `=1/3pir^2h`
`=1/3pixx(4)^2h` ...(2)
Since hollow sphere is melted into a cone so there volumes are equal
(1) = (2)
⇒ `4/3 pi xx (4^3 - 2^3) = 1/3 pi xx 4^2 xx h`
⇒ `4 xx (64 - 8) = 16 xx h`
⇒ h = 14
Therefore, the height of the cone so obtained will have a height of 14 cm.
APPEARS IN
RELATED QUESTIONS
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.) [use `pi = 22/7`]
A 16m deep well with diameter 3.5m is dug up and the earth from it is spread evenly to form a platform 27.5m by 7m. Find height of platform?
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball is dropped into the tube and the level of the water is raised by 6.75cm.Find the radius of the ball .
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
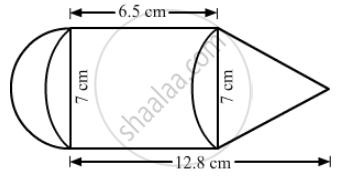
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
How many lead balls, each of radius 1 cm, can be made from a sphere of radius 8 cm?
The volumes of two cubes are in the ratio 1 : 27. The ratio of their surface area is
A metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm. The radius of the base of this cone is
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone.
Find the volume of a solid hemisphere whose total surface area is 462 sq.m.
