Advertisements
Advertisements
Question
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball is dropped into the tube and the level of the water is raised by 6.75cm.Find the radius of the ball .
Solution
Given that radius of a cylindrical tube (r) =12cm
Level of water raised in tube(h)= 6.75cm
Volume of cylinder = πr2h
= π (12)2 x 6.75cm3
=`22/7(12)^2 6.25cm^3` ..........(1)
Let ‘r’ be radius of a spherical ball
Volume of sphere=`4/3pir^3` ...........(2)
To find radius of spherical balls
Equating (1) and (2)
=`pixx(12)^2xx6.75=4/3pir^3`
`r^3=(pixx(12)^2xx6.75)/(4/3xxpi)`
r3 = 729
r3 = 93
r = 9cm
∴Radius of spherical ball(r) = 9cm
APPEARS IN
RELATED QUESTIONS
A hollow sphere of internal and external radii 2cm and 4cm is melted into a cone of basse radius 4cm. find the height and slant height of the cone______?
A reservoir in the form of the frustum of a right circular cone contains 44 × 107 litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take: π = 22/7)
A hemispherical tank, of diameter 3 m, is full of water. It is being emptied by a pipe at the rate of \[3\frac{4}{7}\] litre per second. How much time will it take to make the tank half empty?\[\left[ Use \pi = \frac{22}{7} \right]\]
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, then find the volume of wood in the toy.
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
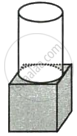
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
Find the perimeter and area of the shaded portion of the following diagram; give your answer correct to 3 significant figures. (Take π = 22/7).
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.
A solid is in the shape of a cone standing on a hemisphere with both their diameters being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid. [Use π = 3.14]
