Advertisements
Advertisements
Question
A reservoir in the form of the frustum of a right circular cone contains 44 × 107 litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take: π = 22/7)
Solution
Let the depth of the frustum cone like reservoir is hm. The radii of the top and bottom circles of the frustum cone like reservoir are r1 =100m and r2 =50m respectively.
The volume of the reservoir is
`V=1/3pi(r_1^2+r_1r_2+r_2^2)xxh`
`=1/3pi(100^2+100xx50+50^2)xxh`
`=1/3xx22/7xx17500xxh`
`=1/3xx22xx2500xxh m^3`
`=1/3xx22xx2500xxhxx10^6 cm^3`
`=1/3xx22xx2500xxhxx10^3` liters
Given that the volume of the reservoir is44x107. Thus, we have
`1/3xx22xx2500xxhxx10^3=44xx10^7`
⇒ `h=(3xx44xx10^7)/(22xx2500xx10^3)`
⇒ h = 24
Hence, the depth of water in the reservoir is 24 m
The slant height of the reservoir is
`l=sqrt((r_1-r_2)^2+h^2)`
`=sqrt((100-50)^2+24^2)`
`=sqrt(3076)`
= 55.46169 meter
The lateral surface area of the reservoir is
`S_1=pi(r_1+r_2)xxl`
= π x (100+50) x 55.46169
= π x 150 x 55.46169
= 26145.225 m2
Hence, the lateral surface area is 26145.225 m2
APPEARS IN
RELATED QUESTIONS
A hemispherical tank, of diameter 3 m, is full of water. It is being emptied by a pipe at the rate of \[3\frac{4}{7}\] litre per second. How much time will it take to make the tank half empty?\[\left[ Use \pi = \frac{22}{7} \right]\]
12 spheres of the same size are made from melting a solid cylinder of 16 cm diameter and 2 cm height. The diameter of each sphere is
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
Three cubes of a metal whose edges are in the ratio 3 : 4 : 5 are melted and converted into a single cube whose diagonal is `12sqrt(3)` cm. Find the edges of the three cubes.
Choose the correct answer of the following question:
If the radius of a sphere becomes 3 times, then its volume will become
A solid rectangular block of dimensions 4.4 m, 2.6 m and 1 m is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
The boundary of the shaded region in the given diagram consists of three semicircular areas, the smaller ones being equal and it’s diameter 5 cm, if the diameter of the larger one is 10 cm,
calculate:
(i) The length of the boundary,
(ii) The area of the shaded region. (Take π = 3.14)

Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is ______.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder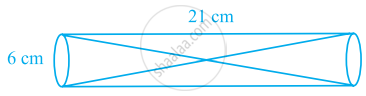
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone.
