Advertisements
Advertisements
Question
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.
Solution
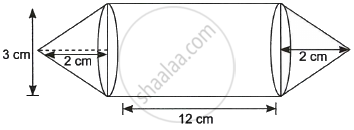
Given, height of each cone (h) = 2 cm
Total Length of model = 12 cm
Diameter of model = 3 cm
Now, Length of cylinder (H) = Total length of model – 2 × height of cone
= 12 – 2 × 2
= 12 – 4
= 8 cm
and radius of cone = radius of cylinder (s)
= `"Diameter of model"/2`
= `3/2` cm
Now, volume of the model = Volume of cylinder + 2 × Volume of cone
= πr2H + 2 × `1/3` πr2h
= πr2`("H" + 2/3)"h"`
= `22/7xx(3/2)^2xx(8+2/3xx2)`
= `22/7xx9/4xx(24+4)/3`
= `(3xx22xx28)/(7xx4)`
= 66 cm3
APPEARS IN
RELATED QUESTIONS
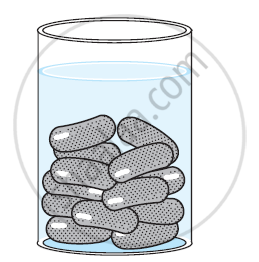
A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see the given figure). Use [π = 22/7]
How many spherical bullets each of 5cm in diameter can be cast from a rectangular block of metal 11 dm x 1m x 5 dm?
A metallic right circular cone 20cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to base. If frustum so obtained bee
drawn into a wire of diameter
(1/16) cm find length of the wire?
A solid right circular cone of height 60 cm and radius 30 cm is dropped in a right circular cylinder full of water, of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
A copper sphere of diameter 18 cm is drawn into a wire of diameter 4 mm. Find the length of the wire.
The ratio of the volumes of two spheres is 8 : 27. If r and R are the radii of spheres respectively, then (R – r) : r is ______.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
The largest sphere is carved out of a solid cube of side 21 cm. Find the volume of the sphere.
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.