Advertisements
Advertisements
Question
A solid right circular cone of height 60 cm and radius 30 cm is dropped in a right circular cylinder full of water, of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres.
Solution
We have,
height of cone, h = 60 cm
the base radius of cone, r =30 cm,
the height of cyllinder, H=180 cm and
the base radius of the cylinder, R = 60 cm
Now,
Volume of water left in the cylinder, = Volume of cylinder - Volume of cone
`= piR^2H-1/3pir^2h`
`= 22/7xx60xx60xx180-1/3xx22/7xx30xx30xx60`
`= 22/7xx30xx30xx60(2xx2xx3-1/3)`
`= 22/7xx54000(12-1/3)`
`=22/7xx54000xx35/3`
`= 1980000 "cm"^3`
`= 1980000/1000000 "m"^3`
`=1.98 "m"^3`
So, the volume of water left in the cylinder is 1.98 m3.
APPEARS IN
RELATED QUESTIONS
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass. [Use π = 3.14]
The diameters of internal and external surfaces of hollow spherical shell are 10cm and 6cm respectively. If it is melted and recast into a solid cylinder of length of 2`2/3`cm, find the
diameter of the cylinder.
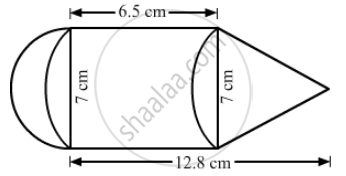
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
The rain water from a 22 m × 20 m roof drains into a cylindrical vessel of diameter 2 m and height 3.5 m. If the rain water collected from the roof fills `4/5` th of the cylindrical vessel, then find the rainfall in centimetre.
The volume of a right circular cylinder with its height equal to the radius is `25"1"/7` cm3. Find the height of the cylinder.
The diameter of the base of a cone is 42 cm and its volume is 12936 cm3. Its height is
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
