Advertisements
Advertisements
Question
The diameter of the base of a cone is 42 cm and its volume is 12936 cm3. Its height is
Options
28 cm
21 cm
35 cm
14 cm
Solution
28 cm
Let h be the height of the cone.
Diameter of the cone = 42 cm
Radius of the cone = 21 cm
Then, volume of the cone`= 1/3 pi"r"^2"h"`
`= 1/3xx22/7xx21xx21xx"h"`
= 22 × 21 × h
Therefore,
22 × 21 × h = 12936
`=> h = ((12936)/(22xx21))`
⇒ h = 28 cm
Hence, the height of the cone is 28 cm.
APPEARS IN
RELATED QUESTIONS
A hollow sphere of internal and external diameter 4cm and 8cm is melted into a cone of base diameter 8cm. Calculate height of cone?
A farmer runs a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
A copper sphere of diameter 18 cm is drawn into a wire of diameter 4 mm. Find the length of the wire.
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
Three cubes of a metal whose edges are in the ratio 3 : 4 : 5 are melted and converted into a single cube whose diagonal is `12sqrt(3)` cm. Find the edges of the three cubes.
A metallic solid right circular cone is of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the
diameter of the sphere.
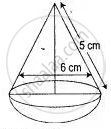
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
