Advertisements
Advertisements
Question
A farmer runs a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Solution
The internal radius of the pipe is 10 cm=0.1 m. The water is flowing in the pipe at 3km/hr = 3000m/hr.
Let the cylindrical tank will be filled in t hours. Therefore, the length of the flowing water in t hours is = 3000 x t meter
Therefore, the volume of the flowing water is V1= π x (0.1)2 x 3000 x t m3
The radius of the cylindrical tank is 5 m and the height is 2 m. Therefore, the volume of the cylindrical tank is
V2 = π x (5)2 x 2 m3
Since, we have considered that the tank will be filled in t hours; therefore the volume of
the flowing water in t hours is same as the volume of the cylindrical tank. Hence, we have
V1 = V2
⇒`pixx(5)^2=pixx(0.1)^2xx3000xxt`
⇒`t=((5)^2xx2)/((0.1)^2xx3000)`
⇒`t=3/5`hours
`t=(5xx60)/3=100` minutes
Hence, the tank will be filled in 1 hour 40 minutes
APPEARS IN
RELATED QUESTIONS
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
A cylindrical road roller made of iron is 1 m long, Its internal diameter is 54 cm and the thickness of the iron sheet used in making the roller is 9 cm. Find the mass of the roller, if 1 cm3 of iron has 7.8 gm mass. (Use π = 3.14)
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π = 22/7).
Two cubes each of volume 125 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
The volumes of two cubes are in the ratio 1 : 27. The ratio of their surface area is
Match the following columns:
| Column I | Column II |
| (a) A solid metallic sphere of radius 8 cm is melted and the material is used to make solid right cones with height 4 cm and base radius of 8 cm. How many cones are formed? | (p) 18 |
| (b) A 20-m-deep well with diameter 14 m is dug up and the earth from digging is evenly spread out to form a platform 44 m by 14 m. The height of the platform is ...........m. |
(q) 8 |
| (c) A sphere of radius 6 cm is melted and recast in the shape of a cylinder of radius 4 cm. Then, the height of the cylinder is ......... cm. |
(r) 16 : 9 |
| (d) The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ....... . |
(s) 5 |
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
Find the minimum length in cm and correct to nearest whole number of the thin metal sheet required to make a hollow and closed cylindrical box of diameter 20 cm and height 35 cm. Given that the width of the metal sheet is 1 m. Also, find the cost of the sheet at the rate of Rs. 56 per m.
Find the area of metal sheet required, if 10% of it is wasted in cutting, overlapping, etc.
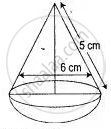
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
Given that 1 cu. cm of marble weighs 25 g, the weight of a marble block of 28 cm in width and 5 cm thick, is 112 kg. The length of the block is ______.
