Advertisements
Advertisements
Question
Find the minimum length in cm and correct to nearest whole number of the thin metal sheet required to make a hollow and closed cylindrical box of diameter 20 cm and height 35 cm. Given that the width of the metal sheet is 1 m. Also, find the cost of the sheet at the rate of Rs. 56 per m.
Find the area of metal sheet required, if 10% of it is wasted in cutting, overlapping, etc.
Solution
Height of the cylindrical box = h = 35 cm
Base radius of the cylindrical box = r = 10 cm
Width of metal sheet = 1 m = 100 cm
Area of metal sheet required = Total surface area of the box
`=>` Length × width = 2πr(r + h)
`=>` Length × 100 = `2 xx 22/7 xx 10(10 + 35) `
`=>` Length × 100 = `2 xx 22/7 xx 10 xx 45`
`=>` Length = `(2 xx 22 xx 10 xx 45)/(100 xx 7)` = 28.28 cm = 28 cm
∴ Area of metal sheet = Length × Width
= 28 × 100
= 2800 cm2
= 0.28 m2
∴ Cost of the sheet at the rate of Rs. 56 per m2
= Rs. (56 × 0.28)
= Rs. 15.68
Let the total sheet required be x.
Then, x – 10% of x = 2800 cm2
`=> x - 10/100 xx x = 2800`
`=> (10x - x)/10 = 2800`
`=> (9x)/10 = 2800`
`=>x = (2800 xx 10)/9`
`=>` x = 3111 cm2
APPEARS IN
RELATED QUESTIONS
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm. Use [π = `22/7`]
How many spherical bullets each of 5cm in diameter can be cast from a rectangular block of metal 11 dm x 1m x 5 dm?
A hemisphere tool of internal radius 9cm is full of liquid. This liquid is to be filled into
cylindrical shaped small bottles each of diameter 3cm and height 4cm. how many bottles are necessary to empty the bowl.
Water in a canal 1.5m wide and 6m deep is flowering with a speed of 10km/ hr. how much area will it irrigate in 30 minutes if 8cm of standing water is desired?
A hemispherical tank, full of water, is emptied by a pipe at the rate of `25/7`litres per sec.
How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m?
From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.
The area of the base of a rectangular tank is 6500 cm2 and the volume of water contained in it is 2.6 m3. The depth of water in the tank is
Match the following columns:
| Column I | Column II |
| (a) A solid metallic sphere of radius 8 cm is melted and the material is used to make solid right cones with height 4 cm and base radius of 8 cm. How many cones are formed? | (p) 18 |
| (b) A 20-m-deep well with diameter 14 m is dug up and the earth from digging is evenly spread out to form a platform 44 m by 14 m. The height of the platform is ...........m. |
(q) 8 |
| (c) A sphere of radius 6 cm is melted and recast in the shape of a cylinder of radius 4 cm. Then, the height of the cylinder is ......... cm. |
(r) 16 : 9 |
| (d) The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ....... . |
(s) 5 |
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
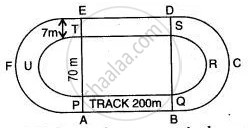
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
