Advertisements
Advertisements
Question
The area of the base of a rectangular tank is 6500 cm2 and the volume of water contained in it is 2.6 m3. The depth of water in the tank is
Options
3.5 m
4 m
5 m
8 m
Solution
4 m
Area of the base of a rectangular tank
= 6500 cm2
`= (6500/(100xx100)) "m"^2`
`= 13/20 "m"^2`
Let the depth of the water be d meters.
Then,
`13/20xx"d"=2.6`
`=> "d" = (26/10xx20/13) "m"`
APPEARS IN
RELATED QUESTIONS
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
A farmer runs a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be 1/125 of the volume of the original cone, determine at what height above the base the section is made.
A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 2.1 cm and the height of the cone is 4 cm. The solid is placed in a cylindrical tub full of water in such a way that the whole solid is submerged in water. If the radius of the cylinder is 5 cm and its height is 9.8 cm, find the volume of the water left in the tub.
Rainfall in an area is 5 cm. The volume of the water that falls on 2 hectares of land is
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
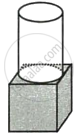
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
In the equilateral Δ ABC of side 14 cm, side BC is the diameter of a semicircle as shown in the figure below. Find the area of the shaded region. (Take π = 22/7 and √3 = 1.732)
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.