Advertisements
Advertisements
Question
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
Solution
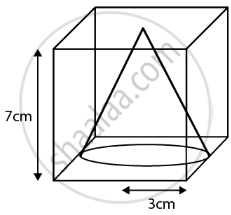
From the figure, we get,
Volume of remaining solid = Volume of cube – Volume of cone
For Cube
Side, a = 7 cm
We know that,
Volume of cube = a3, where a = side of cube
Volume of cube = (7)3 = 343 cm3
For cone
Radius, r = 3 cm
Height, h = 7 cm
Volume of cone = `1/3 π"r"^2"h"`
= `1/3 π(3)^(2)7`
= `3 xx 22/7 xx 7`
= 66 cm3
Volume of remaining solid = Volume of cube – Volume of cone
= 343 – 66
= 277 cm3
APPEARS IN
RELATED QUESTIONS
How many spherical bullets each of 5cm in diameter can be cast from a rectangular block of metal 11 dm x 1m x 5 dm?
A spherical ball of radius 3cm is melted and recast into three spherical balls. The radii of the two of balls are 1.5cm and 2cm . Determine the diameter of the third ball?
A 16m deep well with diameter 3.5m is dug up and the earth from it is spread evenly to form a platform 27.5m by 7m. Find height of platform?
The diameters of the internal and external surfaces of a hollow spherical shell are 6 cm and 10 cm respectively. If it is melted and recast and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder.
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
The volume of a right circular cylinder with its height equal to the radius is `25"1"/7` cm3. Find the height of the cylinder.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is ______.
A solid metal cone with base radius 12 cm and height 24 cm is melted to form solid spherical balls of diameter 6 cm each. Find the number of balls formed.
A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
