Advertisements
Advertisements
Question
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
Solution
According to the question,
We get the figure given below,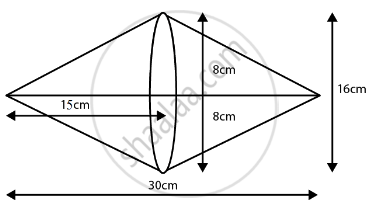
We know that,
Total surface area of shape formed = Curved area of first cone + Curved surface area of second cone
Since, both cones are identical,
We have,
Total surface area of shape formed = Curved area of first cone + Curved surface area of the second cone
= 2(Surface area of cone)
We also know that,
Surface area of cone = πrl, where r = radius and l = slant height
And the total surface area of shape so formed = 2πrl
Given in the question that,
Radius, r = 8 cm
Height, h = 15 cm
Therefore,
Area = Curved area of first cone + Curved surface area of the second cone
= 2(Surface area of the cone)
= 2 × πrl
= `2 xx π xx "r" xx sqrt("r"^2 + "h"^2)`
= `2 xx 22/7 xx 8 xx sqrt(8^2 + 15^2)`
= `50.28 xx sqrt(289)`
= 854.85 cm2
= 855 cm2 ...(Approx)
Hence, the surface area of shape so formed is 855cm2.
APPEARS IN
RELATED QUESTIONS
The largest possible sphere is carved out of a wooden solid cube of side 7 em. Find the volume of the wood left. (Use\[\pi = \frac{22}{7}\]).
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14)
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ₹ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 10 per 100 cm2. (Take π = 3⋅14)
