Advertisements
Advertisements
Question
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14)
Solution
Let the depth of the bucket is h cm. The radii of the top and bottom circles of the frustum bucket are r1 =20cm and r2 =12cm respectively.
The volume/capacity of the bucket is
`"V" = (1)/(3)π("r"_1^2 + "r"_1"r"_2 + "r"_2^2) xx "h"`
= `(1)/(3)π(20^2 + 20 xx 12 + 12^2) xx "h"`
= `(1)/(3) xx (22)/(7) xx 784 xx "h"`
= `1/3xx22xx112xx"h" "cm"^3`
Given that the capacity of the bucket is 12308.8 Cubic cm. Thus, we have
`(1)/(3) xx 22 xx 112 xx "h" = 12308.8`
⇒ `"h" = (12308.8 xx 3)/(22 xx 112)`
⇒ h = 15
Hence, the height of the bucket is 15 cm
The slant height of the bucket is
`"l" = sqrt(("r"_1 -"r"_2)^2 + "h"^2`
= `sqrt((20 -12)^2 + 15^2)`
= `sqrt(289)`
= 17cm
The surface area of the used metal sheet to make the bucket is
`"S"_1 = π("r"_1 +"r"_2) xx l + π"r"_2^2`
= π x (20 + 12) x 17 + π x 122
= π x 32 x 17 + 144π
= 2160.32cm2
Hence Surface area of the metal = 2160.32cm2
APPEARS IN
RELATED QUESTIONS
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
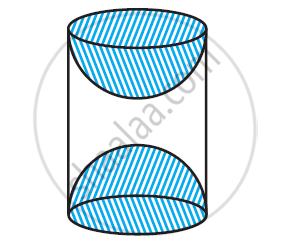
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
From a solid right circular cylinder of height 2.4 cm and radius 0.7 cm, a right circular cone of same height and same radius is cut out. Find the total surface area of the remaining solid.
The internal and external diameters of a hollow hemisphere vessel are 21cm and 25.2 cm The cost of painting 1cm2 of the surface is 10paise. Find total cost to paint the vessel all
over______?
A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of cone are 6cm and 4cm. determine surface area of toy?
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
