Advertisements
Advertisements
Question
A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of cone are 6cm and 4cm. determine surface area of toy?
Solution
Given height of cone (h) = 4cm
Diameter of cone (d) = 6cm
∴Radius (r) =`6/2 =3 cm`
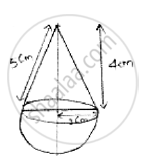
Let ‘l’ be slant height of cone
`l=sqrt(r^2+h^2)`
`=sqrt(3^2+4^2) =5cm`
l = 5cm
∴ Slant height of cone (l) = 5cm.
Curved surface area of cone (S1) = πrl
S1 = π(3)(5) = 47.1cm2
Curved surface area of hemisphere (S2) = 2πr2
`S_2=2pi(3)^2=56.52cm^2`
∴Total surface area(S) = S1 + S2
= 47.1 + 56.52
= 103.62cm2
∴ Curved surface area of toy = 103.62cm2
APPEARS IN
RELATED QUESTIONS
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. `("use " pi=22/7)`
A right circular cone of radius 3 cm, has a curved surface area of 47.1 cm2. Find the volume of the cone. (use π 3.14).
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
A plumbline (sahul) is the combination of (see figure) ______.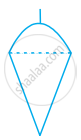
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
