Advertisements
Advertisements
प्रश्न
A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of cone are 6cm and 4cm. determine surface area of toy?
उत्तर
Given height of cone (h) = 4cm
Diameter of cone (d) = 6cm
∴Radius (r) =`6/2 =3 cm`
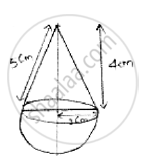
Let ‘l’ be slant height of cone
`l=sqrt(r^2+h^2)`
`=sqrt(3^2+4^2) =5cm`
l = 5cm
∴ Slant height of cone (l) = 5cm.
Curved surface area of cone (S1) = πrl
S1 = π(3)(5) = 47.1cm2
Curved surface area of hemisphere (S2) = 2πr2
`S_2=2pi(3)^2=56.52cm^2`
∴Total surface area(S) = S1 + S2
= 47.1 + 56.52
= 103.62cm2
∴ Curved surface area of toy = 103.62cm2
संबंधित प्रश्न
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)

From a solid right circular cylinder of height 2.4 cm and radius 0.7 cm, a right circular cone of same height and same radius is cut out. Find the total surface area of the remaining solid.
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid.
From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of the cylindrical part are 3 m and 14 m respectively, and the total height of the tent is 13.5 m, find the area of the canvas required for making the tent, keeping a provision of 26 m2 of canvas for stitching and wastage. Also, find the cost of the canvas to be purchased at the rate of ₹ 500 per m2.
