Advertisements
Advertisements
Question
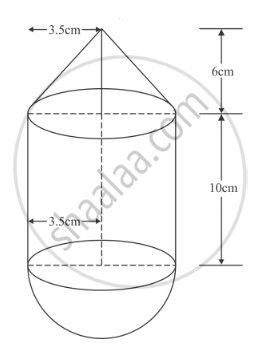
A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm. and 6 cm, respectively. Find the total surface area of the solid. (Use π =`22/7`)
Solution
Given,
Radius of the common base(r) = 3.5 cm
Height of the cylindrical part (h) = 10 cm
Height of the conical part (H) = 6 cm
Let 'l' be the slant height of the cone
Then, we know that,
I2 = r2 + H2
I2 = 3.52 + 62
= 12.25 + 36
= 48.25
l = 6.95 cm
So, the curved surface area of the cone (S1) = πrl
S1 = π(3.5)(6.95)
S1 = `22/7 xx 3.5 xx 6.95`
S1 = 76.45 cm2
Curved surface area of cylinder (S2) = 2πrh
S2 = 2π(3.5)(10)
S2 = `2 xx 22/7 xx 3.5 xx 10`
S2 = 220 cm2
Curved surface area of hemisphere(S3) = 2πr2
S3 = `2 xx 22/7 xx 3.5^2`
S3 = 77 cm2
Total surface area of the solid is given by
S = S1 + S2 +S3
= 76.45 + 220 + 77
= 373.45 cm2
RELATED QUESTIONS
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation?
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the top (Use π = 22/7)
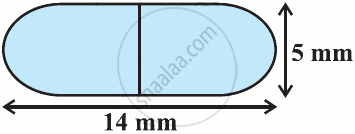
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimension 6cm \[\times\] 42cm \[\times\] 21 cm.
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid.
Three solid spheres of radii 3, 4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
From a solid cube of side 7 cm , a conical cavity of height 7 cm and radius 3 cm is hollowed out . Find the volume of the remaining solid.
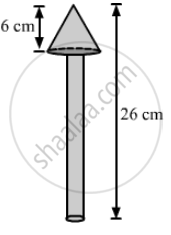
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`