Advertisements
Advertisements
Question
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
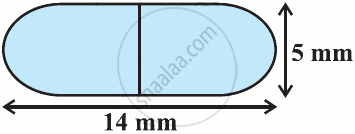
Solution
It can be observed that
Radius (r) of cylindrical part = Radius (r) of hemispherical part
= `"Diameter of the capsule"/2`
= `5/2`
= 2.5 mm
Length of cylindrical part (h) = Length of the entire capsule − 2 × r
= 14 − 2 × 2.5
= 9 mm
Surface area of capsule = 2 × CSA of hemispherical part + CSA of cylindrical part
= 2 × 2πr2 + 2πrh
`= 4pi(5/2)^2 + 2pi(5/2)(9)`
= 25π + 45π
= 70π mm2
= `70 xx 22/7`
= 220 mm2
APPEARS IN
RELATED QUESTIONS
If the total surface area of a solid hemisphere is 462 cm2 , find its volume.[Take π=22/7]
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation?
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)

2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
A vessel is in the form of hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. `[\text{Use}pi=22/7]`
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is:
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of these balls are 1.5 cm and 2 cm. Find the radius of the third ball.
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
The volume of a hemisphere is 19404 cm3. The total surface area of the hemisphere is
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ₹ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 10 per 100 cm2. (Take π = 3⋅14)
The radius of spherical balloon increases from 8 cm to 12 cm. The ratio of the surface areas of balloon in two cases is ______.
A plumbline (sahul) is the combination of (see figure) ______.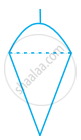
Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is 6πr2.
The total surface area of a solid hemisphere of radius 7 cm is ______.
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
