Advertisements
Advertisements
Question
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is:
Options
1 : 2
2 : 1
1 : 4
4 : 1
Solution
Let the radius and height of the original cylinder be r and h respectively.
∴Volume of the original cylinder = πr2h
According to the question, radius of the new cylinder is halved keeping the height same.
⇒ Radius of the new cylinder`=r/2`
Also, height of the new cylinder = h
∴ Volume of the new cylinder `pi(r/2)^2h=(pir^2h)/4`
`\text{Volume of the new cylinder}/\text{Volume of original cylinder}=(((pir^2h)/4))/(r^2h4)=underline1=1:4`
Hence, the correct answer is C.
APPEARS IN
RELATED QUESTIONS
The largest possible sphere is carved out of a wooden solid cube of side 7 em. Find the volume of the wood left. (Use\[\pi = \frac{22}{7}\]).
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
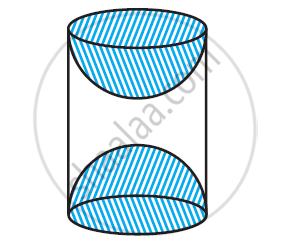
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
