Advertisements
Advertisements
प्रश्न
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is:
पर्याय
1 : 2
2 : 1
1 : 4
4 : 1
Advertisements
उत्तर
Let the radius and height of the original cylinder be r and h respectively.
∴Volume of the original cylinder = πr2h
According to the question, radius of the new cylinder is halved keeping the height same.
⇒ Radius of the new cylinder`=r/2`
Also, height of the new cylinder = h
∴ Volume of the new cylinder `pi(r/2)^2h=(pir^2h)/4`
`\text{Volume of the new cylinder}/\text{Volume of original cylinder}=(((pir^2h)/4))/(r^2h4)=underline1=1:4`
Hence, the correct answer is C.
APPEARS IN
संबंधित प्रश्न
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, ∠ DAB = 900, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π=22/7]
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. `("use " pi=22/7)`
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)
A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of cone are 6cm and 4cm. determine surface area of toy?
A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm, and height 3 cm. Find the area of its whole surface and volume.
The radii of the circular bases of a frustum of a right circular cone are 12 cm and 3 cm and the height is 12 cm. Find the total surface area and the volume of the frustum.
In Figure 4, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region.\[[Use\pi = 3 . 14]\]
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
In a right circular cone, the cross-section made by a plane parallel to the base is a
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ₹ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 10 per 100 cm2. (Take π = 3⋅14)
Eight solid sphere of same size are made by melting a solid metallic cylinder of base diameter 6 cm and height 32 cm. The diameter of each sphere is ______.
If two solid hemispheres of the same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
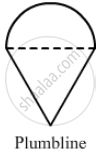
A plumbline (sahul) is the combination of (see figure) ______.
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
|
Khurja is a city in the Indian state of Uttar Pradesh famous for the pottery. Khurja pottery is traditional Indian pottery work which has attracted Indians as well as foreigners with a variety of tea sets, crockery and ceramic tile works. A huge portion of the ceramics used in the country is supplied by Khurja and is also referred as "The Ceramic Town". One of the private schools of Bulandshahr organised an Educational Tour for class 10 students to Khurja. Students were very excited about the trip. Following are the few pottery objects of Khurja.
Students found the shapes of the objects very interesting and they could easily relate them with mathematical shapes viz sphere, hemisphere, cylinder etc. |
Maths teacher who was accompanying the students asked the following questions:
- The internal radius of hemispherical bowl (filled completely with water) in I is 9 cm and the radius and height of the cylindrical jar in II are 1.5 cm and 4 cm respectively. If the hemispherical bowl is to be emptied in cylindrical jars, then how many cylindrical jars are required?
- If in the cylindrical jar full of water, a conical funnel of the same height and same diameter is immersed, then how much water will flow out of the jar?
