Advertisements
Advertisements
प्रश्न
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
उत्तर
Given,
The outer and inner diameters of pipe are 8 cm and 7 cm.
Dimensions of a solid cuboid of iron = 53 cm × 40 cm × 15 cm.
When a shape melted and recast into another shape volume will remain same.
Volume of cubical iron = volume of cylindrical pipe
length × breadth × height = π(R2 − r2)h
53 × 40 × 15 = `22/7 xx (4^2 - (7/2)^2)h`
53 × 40 × 15 = `22/7 xx 15/4 xx h`
h = `(53 xx 40 xx 15 xx 7 xx 4)/(22 xx 15)`
h = 2698.18 cm = 27 m [∵ 1 m = 100 cm]
APPEARS IN
संबंधित प्रश्न
The largest possible sphere is carved out of a wooden solid cube of side 7 em. Find the volume of the wood left. (Use\[\pi = \frac{22}{7}\]).
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
Water in a canal, 5·4 m wide and 1·8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
From a solid right circular cylinder of height 2.4 cm and radius 0.7 cm, a right circular cone of same height and same radius is cut out. Find the total surface area of the remaining solid.
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is:
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
A copper wire of diameter 6 mm is evenly wrapped on a cylinder of length 18 cm and diameter 49 cm to cover its whole surface. Find the length and the volume of the wire. If the density of the copper be 8.8 g per cm3, then find the weight of the wire.
The radius of spherical balloon increases from 8 cm to 12 cm. The ratio of the surface areas of balloon in two cases is ______.
Tamper-proof tetra-packed milk guarantees both freshness and security. This milk ensures uncompromised quality, preserving the nutritional values within and making it a reliable choice for health-conscious individuals.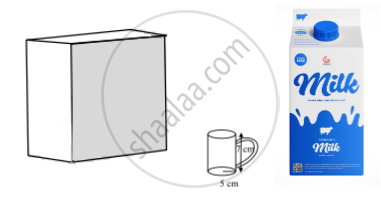
500 ml milk is packed in a cuboidal container of dimensions 15 cm × 8 cm × 5 cm. These milk packets are then packed in cuboidal cartons of dimensions 30 cm × 32 cm × 15 cm.
Based on the above-given information, answer the following questions:
i. Find the volume of the cuboidal carton. (1)
ii. a. Find the total surface area of the milk packet. (2)
OR
b. How many milk packets can be filled in a carton? (2)
iii. How much milk can the cup (as shown in the figure) hold? (1)
